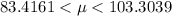1 Answer

Zato · Answer 1 · 2020-03-14T08:56:42+0000

Answer with explanation:

The confidence interval for population mean (when population standard deviation is unknown) is given by :-

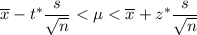
$\overline{x}-t^*(s)/(√(n))< \mu<\overline{x}+z^*(s)/(√(n))$

, where n= sample size

$\overline{x}$ = Sample mean

s= sample size

t* = Critical value.

Given : n= 25

Degree of freedom :
df=n-1=24

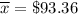
$\overline{x}= \$93.36$

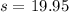
$s=\ $19.95$

Significance level for 98% confidence interval :
$\alpha=1-0.98=0.02$

Using t-distribution table ,

Two-tailed critical value for 98% confidence interval :

$t^*=t_(\alpha/2,\ df)=t_(0.01,\ 24)=2.4922$

⇒ The critical value that should be used in constructing the confidence interval = 2.4922

Then, the 95% confidence interval would be :-

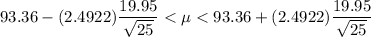
$93.36-(2.4922)(19.95)/(√(25))< \mu<93.36+(2.4922)(19.95)/(√(25))$

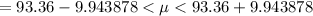
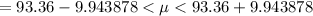
$=93.36-9.943878< \mu<93.36+9.943878$

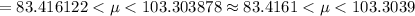
$=83.416122< \mu<103.303878\approx83.4161<\mu<103.3039$

Hence, the 98% confidence interval for the mean repair cost for the dryers. =
$83.4161<\mu<103.3039$