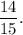Answer: The required probability is
Step-by-step explanation: Given that the probabilities that A, B and C can solve a particular problem are
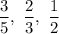 respectively.
respectively.
We are to determine the probability that at least one of the group solves the problem , if they all try.
Let E, F and G represents the probabilities that the problem is solved by A, B and C respectively.
Then, according to the given information, we have
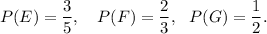
So, the probabilities that the problem is not solved by A, not solved by B and not solved by C are given by

Since A, B and C try to solve the problem independently, so the probability that the problem is not solved by all of them is

Therefore, the probability that at least one of the group solves the problem is
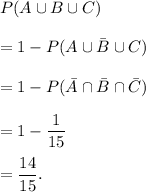
Thus, the required probability is