Question

Solve the equation by first using a Sum-to-Product Formula. (Enter your answers as a comma-separated list. Let k be any integer. Round terms to three decimal places where appropriate.) sin(5θ) − sin(3θ) = cos(4θ)

Answer 1

Solutions of the equation are 22.5°, 30°.

Explanation:

The given equation is sin(5θ) - sin(3θ) = cos(4θ)

We take left side of the equation

sin(5θ) - sin(3θ) =
`2cos((5\theta+3\theta)/(2))sin((5\theta-3\theta)/(2))`

=
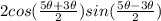
`2cos(4\theta)sin(\theta)` [From sum-product identity]

Now we can write the equation as

2cos(4θ)sin(θ) = cos(4θ)

2cos(4θ)sinθ - cos(4θ) = 0

cos(4θ)[2sinθ - 1] = 0

cos(4θ) = 0

4θ = 90°

θ =
`(90)/(4)`

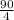
θ = 22.5°

and (2sinθ - 1) = 0

sinθ =
`(1)/(2)`

θ = 30°

Therefore, solutions of the equation are 22.5°, 30°