Answer:
The amount of money in Victoria's account at the end of n-th year will be,
$
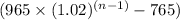
Explanation:
The amount of money in Victoria's account at the end of n-th year will be,
$
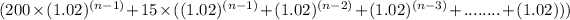
= $
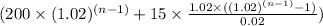
= $
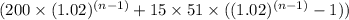
= $
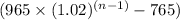
Since, the interest is compounded over that $ 200 (which was there in the account at the end of 1st year) for (n-1) years and for (n-1) years, (n-2) years, (n -3) years, ...... 1 year respectively over those $ 15 which are deposited in the account at the end of 1 , 2, 3, ...... (n-1) years.