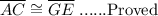Question

How does this get solved? I am a bit confused on what to do next. Help is very appreciated.

Answer 1

The Proof is given below.

Explanation:

Given:

AD ≅ BD ≅ FD ≅ GD

To Prove:

AC ≅ GE

Proof:

In Δ ADF and Δ GDB

AD ≅ DG ……….{Given}

∠ ADF ≅ ∠ BDG …………..{Vertically Opposite angles are equal}

FD ≅ BD ……….{Given}

Δ ADF ≅ Δ GDB ….{Side-Angle-Side test}

∴∠ FAD ≅ ∠ BGD .....{corresponding angles of Congruent Triangle ( c.p.c.t}

i.e ∠ CAD ≅ ∠ EGD.....{ F-C-A and B-E-G straight line}.......( 1 )

Now ,

In Δ CAD and Δ E GD

∠ CAD ≅ ∠ EGD ……….{From ( 1 ) above}

AD ≅ GD ……….{Given}

∠ ADC ≅ ∠ EDG …………..{Vertically Opposite angles are equal}

Δ ADF ≅ Δ GDB ….{Angle-Side-Angle test}

∴ AC ≅ GE .....{corresponding sides of Congruent Triangle ( c.p.c.t}

`\overline {AC} \cong \overline{GE}\ \textrm{......Proved}`