Question

What is the product?

(negative 3 s + 2 t)(4 s minus t)

negative 12 s squared minus 2 t squared
negative 12 s squared + 2 t squared
negative 12 s squared + 8 s t minus 2 t squared
negative 12 s squared + 11 s t minus 2 t squared

Answer 1

option 4 is the answer

Explanation:

Answer 2

(d) negative 12 s squared + 11 s t minus 2 t squared is the PRODUCT.

Explanation:

Here, the given expression is:

(negative 3 s + 2 t)(4 s minus t) = (- 3s + 2t) (4s - t)

Now, by DISTRIBUTIVE PROPERTY:

A(B-C) = AB - AC

Simplifying the given expression ,we get:

`(- 3s + 2t) (4s - t)  = -3s(4s-t) + 2t(4s -t)\\= -3s(4s) -3s(-t) + 2t(4s) + 2t(-t)  = -12s^2 + 3st + 8 st - 2t^2\\= -12s^2 + 11st - 2t^2\\\implies (- 3s + 2t) (4s - t)  =   -12s^2 + 11st - 2t^2`

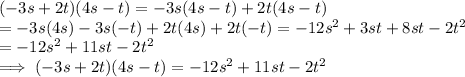
Now, the resultant expression can also be written as

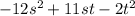`-12s^2 + 11st - 2t^2` = negative 12 s squared + 11 s t minus 2 t squared.

Hence, the option (4) is the correct option.