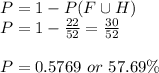Answer:
30/52 or 0.5769 or 57.69%
Explanation:
In a standard deck of 52 cards, the number of face cards (F) and the number of hearts (H) is given by:
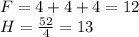
Out of all hearts, three of them are face cards (jack, king, and queen). Therefore, the probability of a card being EITHER a face card or a heart is:
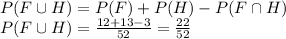
Therefore, the probability of card being NEITHER a face card NOR a heart is: