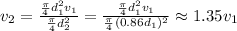Answer:
The speed in the smaller section is

Step-by-step explanation:
Assuming all the parts of the pipe are at the same height, we can use continuity equation for incompressible fluids:
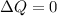 (1)
(1)
With Q the flux of water that is
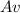 with A the cross section area and v the velocity, so by (1):
with A the cross section area and v the velocity, so by (1):
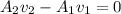
subscript 2 is for the smaller section and 1 for the larger section, solving for
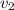 :
:
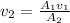 (2)
(2)
The cross section areas of the pipe are:
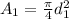
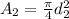
but the problem states that the diameter decreases 86% so
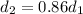 , using this on (2):
, using this on (2):