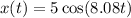Question

A spring has a 12 cm length. When a 200-g mass is hung from the spring, it extends to 27 cm. The hanging mass were pulled downward a further 5 cm. What is the time-dependent function of the position, in centimeters, of the mass, assuming that the phase angle LaTeX: \phi=0ϕ=0?

LaTeX: x(t)=15\cos{(8.08\textrm{ }t)}x(t)=15cos⁡(8.08 t), where the coefficient inside the trigonometric function has units of rad/s.

LaTeX: x(t)=5\cos{(8.08\textrm{ }t)}x(t)=5cos⁡(8.08 t), where the coefficient inside the trigonometric function has units of rad/s.

LaTeX: x(t)=5\cos{(1.29\textrm{ }t)}x(t)=5cos⁡(1.29 t)x(t)=5cos⁡(1.29 t), where the coefficient inside the trigonometric function has units of rad/s.

LaTeX: x(t)=15\cos{(1.29\textrm{ }t)}x(t)=15cos⁡(1.29 t)x(t)=15cos⁡(1.29 t), where the coefficient inside the trigonometric function has units of rad/s.

Answer 1

The equation of the time-dependent function of the position is
`x(t)=5\cos(8.08t)`

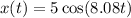
(b) is correct option.

Step-by-step explanation:

Given that,

Length = 12 cm

Mass = 200 g

Extend distance = 27 cm

Distance = 5 cm

Phase angle =0°

We need to calculate the spring constant

Using formula of restoring force

`F=kx`

`mg=kx`

`k=(mg)/(x)`

`k=(200*10^(-3)*9.8)/((27-12)*10^(2))`

`k=13.06\ N/m`

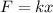
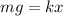
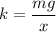
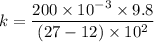
We need to calculate the time period

Using formula of time period

`T=2\pi\sqrt{(m)/(k)}`

Put the value into the formula

`T=2\pi\sqrt{(0.2)/(13.6)}`

`T=0.777\ sec`

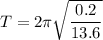
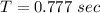
At t = 0, the maximum displacement was 5 cm

So, The equation of the time-dependent function of the position

`x(t)=A\cos(\omega t)`

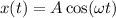
Put the value into the formula

`x(t)=5\cos(2\pi* f* t)`

`x(t)=5\cos(2\pi*(1)/(T)* t)`

`x(t)=5\cos(2\pi*(1)/(0.777)* t)`

`x(t)=5\cos(8.08t)`

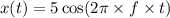
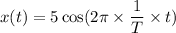
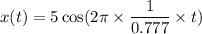
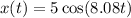
Hence, The equation of the time-dependent function of the position is
`x(t)=5\cos(8.08t)`