Question

A multiple choice test consists of 60 questions. Each question has 4 possible answers of which one is correct. If all answers are random guesses, estimate the probability of getting at least 20% correct. 0.1492 0.3508 0.0901 0.8508 Normal approximation is not suitable.

Answer 1

Option 4 - 0.8508

Explanation:

Given : A multiple choice test consists of 60 questions. Each question has 4 possible answers of which one is correct. If all answers are random guesses.

To find : Estimate the probability of getting at least 20% correct ?

Solution :

20% correct out of 60,

i.e.
`20\%* 60=(20)/(100)* 60=12`

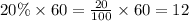
Minimum of 12 correct out of 60 i.e. x=12

Each question has 4 possible answers of which one is correct.

i.e. probability of answering question correctly is
`p=(1)/(4)=0.25`

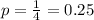
Total question n=60.

Using a binomial distribution,

`P(X\geq 12)=1-P(X\leq 11)`

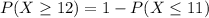
`P(X\geq 12)=1-[P(X=0)+P(X=1)+P(X=0)+P(X=1)+P(X=2)+P(X=3)+P(X=4)+P(X=5)+P(X=6)+P(X=7)+P(X=8)+P(X=9)+P(X=10)+P(X=11)]`

`P(X\geq 12)=1- [^(60)C_0(0.25)^0(1-0.25)+^(60-0)+^(60)C_1(0.25)^1(1-0.25)^(60-1)+^(60-1)+^(60)C_2(0.25)^2(1-0.25)^(60-2)+^(60)C_3(0.25)^3(1-0.25)^(60-3)+^(60)C_4(0.25)^4(1-0.25)^(60-4)+^(60)C_5(0.25)^5(1-0.25)^(60-5)+^(60)C_6(0.25)^6(1-0.25)^(60-6)+^(60)C_7(0.25)^7(1-0.25)^(60-7)+^(60)C_8(0.25)^8(1-0.25)^(60-8)+^(60)C_9(0.25)^9(1-0.25)^(60-9)+^(60)C_(10)(0.25)^(10)(1-0.25)^(60-10)+^(60)C_(11)(0.25)^(11)(1-0.25)^(60-11)]`

`P(X\geq 12)\approx 0.8508`

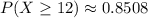
Therefore, option 4 is correct.