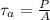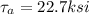Question

Problem 4A titanium [E = 16,500 ksi;  = 5.3×10–6/°F] bar (1) and a bronze [E = 15,200 ksi;  = 12.2×10–6/°F] bar (2), each restrained at one end, are fastened at their free ends by a pin of diameter d = 0.4375 in. The length of bar (1) is L1 = 19 in. and its cross-sectional area is A1 = 0.50 in.2. The length of bar (2) is L2 = 27 in. and its cross-sectional area is A2 = 0.65 in.2. What is the average shear stress in the pin at B if the temperature changes by 40°F?

Answer 1

`\tau_a = 22.7 ksi`

Step-by-step explanation:

Given data:

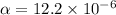`\alpha  = 12.2 * 10^(-6)`degree F

Diameter is d = 0.4375

`L_1 = 19 inch`

`A_1 = 0.50 in^2`

`L_2 = 27 inch`

`A_2 = 0.65 in^2`

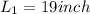
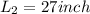
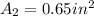
force in titanium and bronze will be equal

from equilibrium condition we have

F_T = F_B = p

From the information given as bar is tightened from ends thus net deformation is assummed to be zero

so we have

`\Delta_T +\Delta_B = \Delta  = 0`

`(PL)/(AE)_T + \alpha \Delta T L = (PL)/(AE)_B + (\alpha \Delta T L)_B`

`(19* P)/(0.5* 16500) + 19 * 5.3* 10^(-6) * 40 = (27P)/(0.65 * 15200) + 27* 12.2* 10^(-6) * 40 = 0`

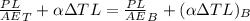
solving for P we get

P = 341 kips

average shear at B

`\tau_a = (P)/(A)`

`\tau_a = (341)/((\pi)/(4) * 0.4375^2)`

`\tau_a = 22.7 ksi`