Question

Earth turns on its axis about once every 24 hours. The Earth's equatorial radius is 6.38 x 106 m. If some catastrophe caused Earth to suddenly come to a screeching halt, with what speed would Earth's inhabitants who live at the equator go flying off Earth's surface?

Answer 1

To solve this problem it is necessary to apply the concepts related to the Period of a body and the relationship between angular velocity and linear velocity.

The angular velocity as a function of the period is described as

`\omega = (2\pi)/(T)`

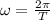
Where,

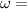`\omega =`Angular velocity

T = Period

At the same time the relationship between Angular velocity and linear velocity is described by the equation.

`v = \omega r`

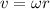
Where,

r = Radius

Our values are given as,

`T = 24 hours`

`T = 24hours ((3600s)/(1 hour))`

`T = 86400s`

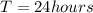
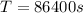
We also know that the radius of the earth (r) is approximately

`6.38*10^6m`

Usando la ecuación de la velocidad angular entonces tenemos que

`\omega = (2\pi)/(T)`

`\omega = (2\pi)/(86400)`

`\omega = 7.272*10^(-5)rad/s`

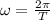
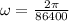
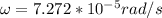
Then the linear velocity would be,

`v = \omega *r`

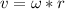
x
`v = \omega *r`

`v= 463.96m/s`

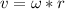
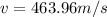
The speed would Earth's inhabitants who live at the equator go flying off Earth's surface is 463.96