Answer:
The final temperature of the given ideal diatomic gas: T₂ = 753.6 K
Step-by-step explanation:
Given: Atmospheric pressure: P = 1.0 atm
Initial Volume: V₁ , Final Volume: V₂ = V₁ (1/10)
⇒ V₁ / V₂ = 10
Initial Temperature: T₁ = 300 K, Final temperature: T₂ = ? K
For a diatomic ideal gas: γ = 7/5
For an adiabatic process:
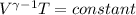
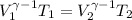
![\left [(V_(1))/(V_(2)) \right ]^(\gamma-1 ) = (T_(2))/(T_(1))](https://img.qammunity.org/2020/formulas/chemistry/high-school/18kjytv9ee6zpjnj1f1i6ng2z1kcwyis96.png)
![\left [10 \right ]^{(7)/(5)-1 } = (T_(2))/(300 K)](https://img.qammunity.org/2020/formulas/chemistry/high-school/gkmj3x7m3uykyrhd56m8ffvij2bypevj8z.png)
![\left [10 \right ]^{(2)/(5) } = (T_(2))/(300 K)](https://img.qammunity.org/2020/formulas/chemistry/high-school/wa31tspcojgjq0f0g5qbeve038ddiugtkd.png)


Therefore, the final temperature of the given ideal diatomic gas: T₂ = 753.6 K