Question

The profit function p(x) of a tour operator is modeled by p(x) = −2x^2 + 700x − 10000, where x is the average number of tours he arranges per day. What is the range of the average number of tours he must arrange per day to earn a monthly profit of at least $50,000?

Answer 1

Answer: between 150 and 200; inclusive

Explanation:

The answer is 'inclusive' NOT 'exclusive.'

Answer 2

Answer: The correct answer is D). Between 150 and 200; exclusive

Explanation:

Given profit function p(x) of a tour operator is modeled by

p(x)=
`(-2)x^(2) +700x-10000`

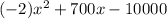
Where, x is the average number of tours he arranges per day.

To find number of tours to arrange per day to get monthly profit of at least 50,000$:

Now, he should make at-least 50000$ profit.

we can write as p(x)>50000$

`(-2)x^(2) +700x-10000\geq50000`

`(-2)x^(2) +700x-60000\geq0`

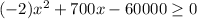
Roots are x is 150 and 200

(x-150)(x-200)>0

Case 1 : x>150 and x>200

x>150 also satisfy the x>200.

Case2: x<100 and x<200

x<200 also satisfy the x<100

Thus, the common range is 150<x<200

The correct answer is D). Between 150 and 200; exclusive