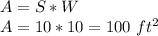Answer:
10 ft x 10 ft
Area = 100 ft^2
Explanation:
Let 'S' be the length of the southern boundary fence and 'W' the length of the eastern and western sides of the fence.
The total area is given by:
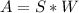
The cost function is given by:
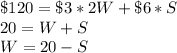
Replacing that relationship into the Area function and finding its derivate, we can find the value of 'S' for which the area is maximized when the derivate equals zero:

If S=10 then W =20 -10 = 10
Therefore, the largest area enclosed by the fence is: