Question

A baseball, which has a mass of 0.685 kg., is moving with a velocity of 38.0 m/s when it contacts the baseball bat duringwhich time the velocity of the ball becomes 57.0 m/s in the opposite direction.a. How much impulse has been delivered to the ball by the bat?While in contact with the bat the ball undergoes a maximum compression of approximately 1.0 cm.b. Approximately how long did it take for the ball to be stopped by the bat?c. What will be the average force applied to the ball by the bat while stopping the ball?

Answer 1

Answers:

a) 65.125 Ns

b) 5.263 * 10^(-4) s

c) 123737.5 N

Step-by-step explanation:

a) Impulse delivered to the ball F.dt

According to the Impulse-Momentum we have the following:

`F*dt = m*(V_(2) - V_(1))`

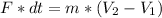
Using the given data we insert in equation above:

`Impulse = 0.685 kg (57 - (-38))\\\\Impulse = 65.1225 Ns`

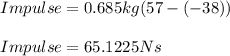
Answer: 65.125 Ns

b)

This time can be calculated by the following equations, taking into account the ball undergoes a maximum compression of approximately 0.01m :

Using the kinematic equations for constant acceleration:

`(v_(f))^2 = (v_(i))^2 + 2*a*s`

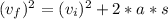
Where:

vf = 0 (ball stops on the bat)

vi = 38 m/s

s = compression = 0.01 m

Using the equation above we compute acceleration:

`a = ((v_(f))^2 - (v_(i))^2)/(2*s) \\\\a = (0^2 - 38^2)/(2*0.01) \\\\a = -72,200 m/s^2`

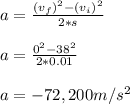
Using the acceleration to compute time:

`v_(f) = v_(i) + a*t\\\\t = (v_(f) - v_(i))/(a)\\\\t = (0 - 38)/(-72,200)\\\\t = 5.263*10^(-4) s`

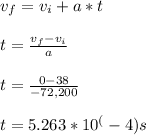
Answer: 5.263*10^(-4) s

c)

According to Newton's second law of motion:

`F_(avg) * dt = Impulse`

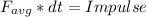
Using answer from part a and b

`F_(avg) = (Impulse)/(dt) \\\\F_(avg) = (65.125)/(5.263*10^(-4)) \\\\F_(avg) = 123737.5 N`

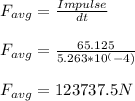
Answer: 123737.5 N

Answer 2

Answers:

a)
`65.075 kgm/s`

b)
`10.526 s`

c)
`61.82 N`

Step-by-step explanation:

a) Impulse delivered to the ball

According to the Impulse-Momentum theorem we have the following:

`I=\Delta p=p_(2)-p_(1)` (1)

Where:

`I` is the impulse

`\Delta p` is the change in momentum

`p_(2)=mV_(2)` is the final momentum of the ball with mass
`m=0.685 kg` and final velocity (to the right)
`V_(2)=57 m/s`

`p_(1)=mV_(1)` is the initial momentum of the ball with initial velocity (to the left)
`V_(1)=-38 m/s`

So:

`I=\Delta p=mV_(2)-mV_(1)` (2)

`I=\Delta p=m(V_(2)-V_(1))` (3)

`I=\Delta p=0.685 kg (57 m/s-(-38 m/s))` (4)

`I=\Delta p=65.075 kg m/s` (5)

b) Time

This time can be calculated by the following equations, taking into account the ball undergoes a maximum compression of approximately
`1.0 cm=0.01 m`:

`V_(2)=V_(1)+at` (6)

`V_(2)^(2)=V_(1)^(2)+2ad` (7)

Where:

`a` is the acceleration

`d=0.01 m` is the length the ball was compressed

`t` is the time

Finding
`a` from (7):

`a=(V_(2)^(2)-V_(1)^(2))/(2d)` (8)

`a=((57 m/s)^(2)-(-38 m/s)^(2))/(2(0.01 m))` (9)

`a=90.25 m/s^(2)` (10)

Substituting (10) in (6):

`57 m/s=-38 m/s+(90.25 m/s^(2))t` (11)

Finding
`t`:

`t=1.052 s` (12)

c) Force applied to the ball by the bat

According to Newton's second law of motion, the force
`F` is proportional to the variation of momentum
`\Delta p` in time
`\Delta t`:

`F=(\Delta p)/(\Delta t)` (13)

`F=(65.075 kgm/s)/(1.052 s)` (14)

Finally:

`F=61.82 N`