Answer:
Option C.
Explanation:
Given information
 and
and

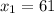 and
and

Using the given information we get
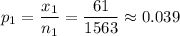
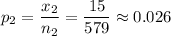
The formula for confidence interval for p_1 - p_2 is
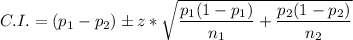
From the standard normal table the value of z* at 95% confidence interval = 1.96.

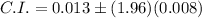
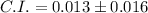
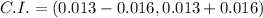
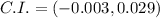
The 95% confidence interval for p_1 - p_2. is (-0.003,0.029).
Therefore, the correct option is C.