Question

If you have 100 g of radio isotope with a half-life of 10 years: How much of the isotope will you have left after 10 years? How much of the isotope will you have left after 20 years? How much of half-lives will occur in 40 years?

Answer 1

1)50.007 grams of an isotope will left after 10 years.

1)25.007 grams of an isotope will left after 20 years.

3) 23 half-lives will occur in 40 years.

Step-by-step explanation:

Formula used :

`N=N_o* e^(-\lambda t)\\\\\lambda =\frac{0.693}{t_{(1)/(2)}}`

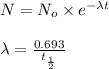
where,

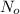`N_o` = initial mass of isotope

N = mass of the parent isotope left after the time, (t)

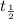`t_{(1)/(2)}` = half life of the isotope

`\lambda` = rate constant

We have:

`[N_o]=100 g`

`t_(1/2)=10 years`

`\lambda =(0.693)/(t_(1/2))=(0.693)/(10 year)=0.0693 year^(-1)`

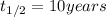
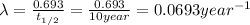
1) mass of isotope left after 10 years:

t = 10 years

`N=N_o* e^(-\lambda t)`

`N=100g* e^{-0.0693 year^(-1)* 10}=50.007 g`

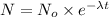
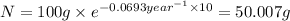
2) mass of isotope left after 20 years:

t = 20 years

`N=N_o* e^(-\lambda t)`

`N=100g* e^{-0.0693 year^(-1)* 20}=25.007 g`

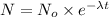
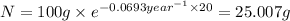
3) Half-lives will occur in 40 years

Mass of isotope left after 40 years:

t = 40 years

`N=N_o* e^(-\lambda t)`

`N=100g* e^{-0.0693 year^(-1)* 40}=6.2537 g`

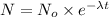
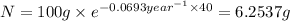
number of half lives = n

`N=(N_o)/(2^n)`

`6.2537 g=(100 g)/(2^n)`

`n\ln 2=(100 g)/(6.2537 g)`

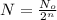
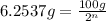
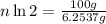
n = 23

23 half-lives will occur in 40 years.