Question

A balloon is filled with 0.250 mole of air at 35°C. If the volume of the balloon is 6.23 liters, what is the absolute pressure of the air in the balloon? The absolute pressure of the air in the balloon is kilopascals.

Answer 1

Answer: 103 for Edmentum users !

Answer 2

102.807 kPa

Step-by-step explanation:

There are some assumptions to be made in the answer. The air inside the balloon acts as an ideal gas at a given temperature conditions.

Using the combined ideal gas equation.

`PV = nRT\\`

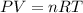
P= absolute pressure of air inside the balloon.

V= volume of air inside the balloon (6.23 L= 6.23 * 10⁻³ m³)

n= moles of gas(air). (0.250 mol)

R= Universal gas constant ( 8.314 J / mol·K)

T= Temperature in Kelvin

T= 35 + 273.15 = 308.15 K

So,
`P = (nRT)/(V)`

`P = (0.250 * 8.314 * 308.15)/(6.23 * 10^(-3) )`

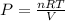
P= 102.807 * 10³ Pa

P= 102.807 kPa