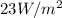Question

Unpolarized light is passed through an optical filter that is oriented in the vertical direction.

If the incident intensity of the light is 46 W/m2 , what is the intensity of the light that emerges from the filter? (Express your answer to two significant figures.)

Answer 1

In order to solve this problem it is necessary to apply the concepts related to intensity and specifically described in Malus's law.

Malus's law warns that

`I = I_0 cos^2\theta`

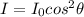
Where,

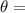`\theta=` Angle between the analyzer axis and the polarization axis

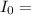`I_0 =`Intensity of the light before passing through the polarizer

The intensity of the beam from the first polarizer is equal to the half of the initial intensity

`I = (I_0)/(2)`

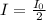
Replacing with our the numerical values we get

`I = (46)/(2)`

`I = 23W/m^2`

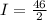
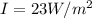
Therefore the intensity of the light that emerges from the filter is
`23W/m^2`