A pressure that will support a column of Hg to a height of 256mm would support a column of water to what height? The density of mercury is 13.6 g/cm3; the density of water is 1.…

Question

asked Apr 17, 2020 2.7k views

1 Answer

Duxa · Answer 1 · 2020-04-22T06:16:52+0000

Answer: Option (A) is the correct answer.

Step-by-step explanation:

It is known that relation between pressure, density, height, and gravity is as follows.

P =
$\rho * g * h$

As it is given that pressure of both mercury and water column are equal. Therefore,

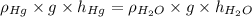
$\rho_(Hg) * g * h_(Hg) =\rho_{H_(2)O} * g * h_{H_(2)O}$

Cancelling the common terms in the formula. Now, putting the given values into the above formula as follows.

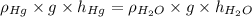
$\rho_(Hg) * g * h_(Hg) =\rho_{H_(2)O} * g * h_{H_(2)O}$

$13.6 g/cm^(3) * 256 mm = 1 * h_{H_(2)O}$

3481.6 mm =
$h_{H_(2)O}$

As 1 mm = 0.1 cm

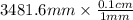
3481.6 mm * (0.1 cm)/(1 mm)

= 348.1 cm

or, = 348 cm (approx)

thus, we can conclude that height of the given column is 348 cm.