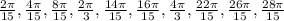Question

Find all the solutions in there interval (0,2pi) for cos5x=-1/2

Answer 1

`(2\pi)/(15),(4\pi)/(15),(8\pi)/(15),(2\pi)/(3),(14\pi)/(15), (16\pi)/(15), (4\pi)/(3),(22\pi)/(15), (26\pi)/(15), (28\pi)/(15)`

Explanation:

Solving trigonometric equations.

We are given a condition and we must find all angles who meet it in the provided interval. Our equation is

`cos5x=-(1)/(2)`

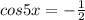
Solving for 5x:

`5x=(2\pi)/(3)+2n\pi`

`5x=(4\pi)/(3)+2n\pi`

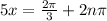
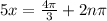
The values for x will be

`x=((2\pi)/(3)+2n\pi)/(5)`

`x=((4\pi)/(3)+2n\pi)/(5)`

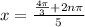
To find all the solutions, we'll give n values of 0, 1, 2,... until x stops belonging to the interval
`(0,2\pi)`

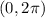
For n=0

`x=((2\pi)/(3))/(5)=(2\pi)/(15)`

`x=((4\pi)/(3))/(5)=(4\pi)/(15)`

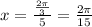
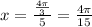
For n=1

`x=((2\pi)/(3)+2\pi)/(5)=(8\pi)/(15)`

`x=((4\pi)/(3)+2\pi)/(5)=(2\pi)/(3)`

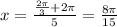
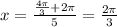
For n=2

`x=((2\pi)/(3)+4\pi)/(5)=(14\pi)/(15)`

`x=((4\pi)/(3)+4\pi)/(5)=(16\pi)/(15)`

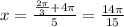
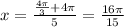
For n=3

`x=((2\pi)/(3)+6\pi)/(5)=(4\pi)/(3)`

`x=((4\pi)/(3)+6\pi)/(5)=(22\pi)/(15)`

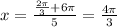
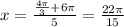
For n=4

`x=((2\pi)/(3)+8\pi)/(5)=(26\pi)/(15)`

`x=((4\pi)/(3)+8\pi)/(5)=(28\pi)/(15)`

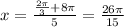
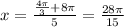
For n=5 we would find values such as

`x=((2\pi)/(3)+10\pi)/(5)=(32\pi)/(15)`

`x=((4\pi)/(3)+10\pi)/(5)=(34\pi)/(15)`

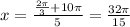
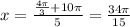
which don't lie in the interval
`(0,2\pi)`

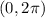
The whole set of results is

`(2\pi)/(15),(4\pi)/(15),(8\pi)/(15),(2\pi)/(3),(14\pi)/(15), (16\pi)/(15), (4\pi)/(3),(22\pi)/(15), (26\pi)/(15), (28\pi)/(15)`