Answer:
(a) The ONLY explicit rule for the nth term of the sequence is
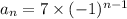 .
.
Explanation:
Here, the given sequence is 7, -7, 7, -7, ...
The first term = 7, Second term = -7, Third term =-7 and so on..
Now check the given sequence for each given formula, we get:
(1)
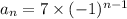
Now, for n = 1 :


Similarly, for, n = 2:
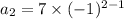
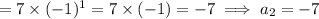
Hence, the given formula satisfies the given sequence.
(2)
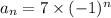
Now, for n = 1 :
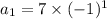
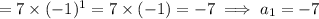
But, First term = 7
Hence, the given formula DO NOT satisfy the given sequence.
(3)
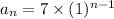
Now, for n = 1 :
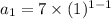
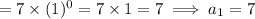
Similarly, for, n = 2:
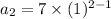
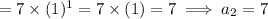
But, Second term = -7
Hence, the given formula DO NOT satisfy the given sequence.
(4)

Now, for n = 1 :

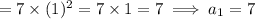
Similarly, for, n = 2:
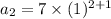
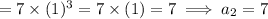
But, Second term = -7
Hence, the given formula DO NOT satisfy the given sequence.
So, the ONLY explicit rule for the nth term of the sequence is
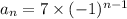 .
.