Answer:
The standard from of the expression is:
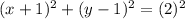
Explanation:
Here the given expression is :

Now, the standard form of a circle is given as :
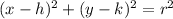
Here, (h,k) = Coordinates of Center, r = Radius
Also, use the algebraic identity:
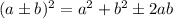
Now, converting the given expression in the standard form, we get:

Add 2 on both sides of the equation, we get:
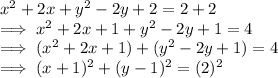
So, here the standard from of the expression is:
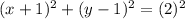
Center coordinates here are (h,k) = ( -1 ,1) and Radius = 2 units