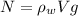Question

g An object with mass m=2 kg is completely submerged, and tethered, to the bottom of a large body of water. If the density of the water is rhow = 1000 kg/m3and the density of the object is rhoob j=500 kg/m3, find the tension in the rope. Take g=10 m/s2and assume the object has a uniform mass density

Answer 1

The tension in the rope is 20 N

Solution:

As per the question:

Mass of the object, M = 2 kg

Density of water,
`\rho_(w) = 1000\ kg/m^(3)`

Density of the object,
`\rho_(ob) = 500\kg/m^(3)`

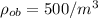
Acceleration due to gravity, g =
`10\ m/s^(2)`

Now,

From the fig.1:

'N' represents the Bouyant force and T represents tension in the rope.

Suppose, the volume of the block be V:

V =
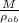`(M)/(\rho_(ob))` (1)

Also, we know that Bouyant force is given by:

`N = \rho_(w)Vg`

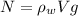
Using eqn (1):

`N = \rho_(w)(M)/(\rho_(ob))g`

`N = 1000(2)/(500)* 10 = 40\ N`

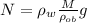
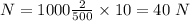
From the fig.1:

N = Mg + T

40 = 2(10) + T

T = 40 - 20 = 20 N

`N = \rho_(w)Vg`