Question

Which is the best interpretation of the solution set for the compound inequality?

3(2x + 1) > 21 or 4x + 3 < 3x +7
no solution
3 Ox<3 or x > 4
all real numbers

Answer 1

For this case we must find the solution set of the given inequalities:

Inequality 1:

`3 (2x + 1)> 21`

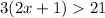
Applying distributive property on the left side of inequality:

`6x + 3> 21`

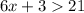
Subtracting 3 from both sides of the inequality:

`6x> 21-3\\6x> 18`

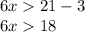
Dividing by 6 on both sides of the inequality:

`x> \frac {18} {6}\\x> 3`

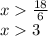
Thus, the solution is given by all the values of "x" greater than 3.

Inequality 2:

`4x + 3 <3x + 7`

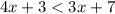
Subtracting 3x from both sides of the inequality:

`4x-3x + 3 <7\\x + 3 <7`

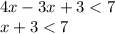
Subtracting 3 from both sides of the inequality:

`x <7-3\\x <4`

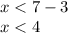
Thus, the solution is given by all values of x less than 4.

The solution set is given by the union of the two solutions, that is, all real numbers.

Answer:

All real numbers