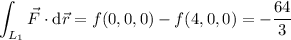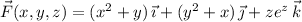
We want to find
 such that
such that
 . This means
. This means
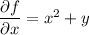
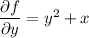
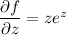
Integrating both sides of the latter equation with respect to
 tells us
tells us
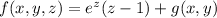
and differentiating with respect to
 gives
gives
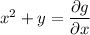
Integrating both sides with respect to
 gives
gives
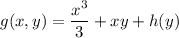
Then
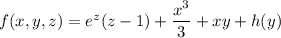
and differentiating both sides with respect to
 gives
gives

So the scalar potential function is
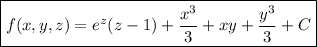
By the fundamental theorem of calculus, the work done by
 along any path depends only on the endpoints of that path. In particular, the work done over the line segment (call it
along any path depends only on the endpoints of that path. In particular, the work done over the line segment (call it
 ) in part (a) is
) in part (a) is
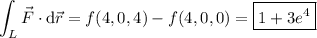
and
 does the same amount of work over both of the other paths.
does the same amount of work over both of the other paths.
In part (b), I don't know what is meant by "df/dt for F"...
In part (c), you're asked to find the work over the 2 parts (call them
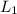 and
and
 ) of the given path. Using the fundamental theorem makes this trivial:
) of the given path. Using the fundamental theorem makes this trivial: