Question

Suppose the scores of students on a Statistics course are Normally distributed with a mean of 563 and a standard deviation of 37. What percentage of the students scored between 563 and 637 on the exam?

Answer 1

47.72% of students scored between 563 and 637 on the exam .

Explanation:

The percentage of the students scored between 563 and 637 on the exam

= The percentage of the students scored lower than 637 on the exam -

the percentage of the students scored lower than 563 on the exam.

Since 563 is the mean score of students on the Statistics course, 50% of students scored lower than 563. that is P(x<563)=0.5

P(x<637)=P(z<z*) where z* is the z-statistic of the score 637.

z score can be calculated using the formula

z*=
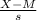`(X-M)/(s)` where

• X =637

• M is the mean score (563)

• s is the standard deviation of the score distribution (37)

Then z*=
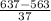`(637-563)/(37)` =2

P(z<2)=0.9772, which means that 97.72% of students scored lower than 637 on the exam.

As a Result, 97.72%-50%=47.72% of students scored between 563 and 637 on the exam