Question

Sometime around 2022, astronomers at the European Southern Observatory hope to begin using the E-ELT(European Extremely Large Telescope), which is planned to have a primary mirror 42 m in diameter. Let us assume that the light it focuses has a wavelength of 600 nm. (1 light-year = 9.461×1015 m) Note: Jupiter's Diameter dj=1.43×108 m 1) What is the most distant Jupiter-sized planet the telescope could resolve, assuming it operates at the diffraction limit? (Express your answer to two significant figures.)

Answer 1

`8.2* 10^(15)\ m`

Step-by-step explanation:

`\lambda` = Wavelength = 600 nm

d = Diameter of mirror = 42 m

D = Distance of object

x = Diameter of Jupiter =
`1.43* 10^8\ m`

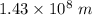
Angular resoulution is given by

`\Delta\theta=1.22(\lambda)/(d)\\\Rightarrow \Delta\theta=1.22(600* 10^(-9))/(42)\\\Rightarrow \Delta\theta=1.74286* 10^(-8)\ rad`

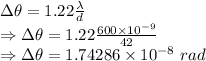
We also have the relation

`\Delta\theta\approx=(x)/(D)\\\Rightarrow D\approx(x)/(\Delta\theta)\\\Rightarrow D\approx(1.43* 10^8)/(1.74286* 10^(-8))\\\Rightarrow D\approx 8.2049* 10^(15)\ m`

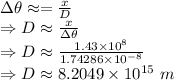
The most distant Jupiter-sized planet the telescope could resolve is
`8.2* 10^(15)\ m`