Question

A mouse is running along the floor in a straight line at 1.3 m/s. A cat runs after it and, perfectly judging the distance d to the mouse ahead, springs up at a speed of 2.5 m/s and an angle 38 degree, landing right on top of the mouse.

What is d, the distance between the cat and mouse at the instant the cat springs into the air?

a)0.931 m

b)0.210 m

c) 0.401 m

d)0.552 m

e)0.641m

Answer 1

Option b

Solution:

As per the question:

Speed of the mouse, v = 1.3 m/s

Speed of the cat, v' = 2.5 m/s

Angle,
`\theta = 38^(\circ)`

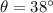
Now,

To calculate the distance between the mouse and the cat:

The distance that the cat moved is given by:

`x = v'cos\theta t`

`x = 2.5cos38^(\circ)* t = 1.97t`

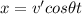
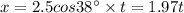
The position of the cat and the mouse can be given by:

`x = x' + vt`

`1.97t = x' + 1.3t`

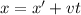
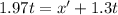
x' = 0.67 t (1)

The initial speed of the cat ahead of the mouse:

u =
`v'sin\theta = 2.5sin38^(\circ) = 1.539\ m/s`

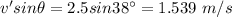
When the time is 0.5t, the speed of the cat is 0, thus:

`0 = u - 0.5tg`

`t = (1.539)/(0.5* 9.8) = 0.314\ s`

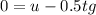
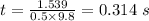
Substituting the value of t in eqn (1):

x' = 0.67(0.314) = 0.210 m

Thus the distance comes out to be 0.210 m