Answer:
x=-4 is a vertical asymptote
Explanation:
A vertical asymptote of the graph of a rational function f(x) is a line x=a, such that one of of these statements is fulfilled
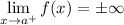
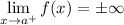
Our function is
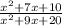
To find the candidate values of a, we set the denominator to zero
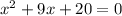
Factoring
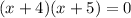
Which gives us two possible vertical asymptotes: x=-4 or x=-5
We now must confirm if one of the two conditions are true for each value of a
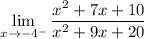
The numerator can be factored as
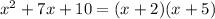
So our limit is
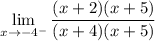
Simplifying:
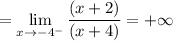
We can see x=-4 is a vertical asymptote
Checking with x=-5, and using the simplified limit:
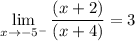
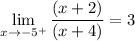
The limit exists and is 3, so x=-5 is NOT a vertical asymptote
The only vertical asymptote of the function is x=4