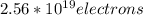Question

A wire carries a current of 4.1 A. How many electrons per second are passing any cross sectional area of the wire? Enter your answer in the format *.**E** (for example, the fundamental unit of charge, which is 1.60 cross 10^(-19) C, would be entered by typing 1.60E-19). electrons per second

Answer 1

To solve this problem it is necessary to apply the concepts related to Current and Load.

The current in terms of the charge of an electron can be expressed as

`i = (q)/(t)`

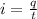
Where,

q = Charge

t = time

At the same time the Charge is the amount of electrons multiplied by the amount of these, that is

q = ne

Replacing in the first equation we have to

`i = (q)/(t)`

`i = (ne)/(t)`

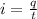
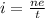
Clearing n,

`n = (it)/(e)`

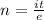
Here the time is one second then

`n = (i)/(e)`

`n = (4.1)/(1.6*10^(-9))`

`n = 2.56*10^(19)electrons`

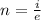
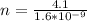
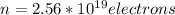
Therefore the number of electrons per second are passing any cross sectional area of the wire are
`2.56*10^(19)electrons`