Question

A theater is selling tickets for a performance. Mr. Smith purchased 8 senior tickets and 5 child tickets for $136 for his friends and family. Mr. Jackson purchased 4 senior tickets and 6 child tickets for $96. What is the price of a senior ticket?

Answer 1

The price of a senior ticket is $12.

Explanation:

Given:

Mr. Smith purchased 8 senior tickets and 5 child tickets for $136. Mr. Jackson purchased 4 senior tickets and 6 child tickets for $96.

Now, to get what is the price of a senior ticket.

Let the senior ticket be
`x` and the child ticket be
`y`:

So, according to question

`8x+5y=136`.........(1)

`4x+6y=96`...........(2)

Now, we have system of equations:

Multiplying the equation (2) by -2 we get:

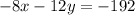`-8x-12y=-192`.......(3)

Now, adding the equation (3) and (1) the variables and the numbers:

`-8x-12y+8x+5y=-192+136`

`-7y=-56`

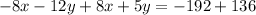
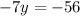
Dividing both sides by -7 we get:

`y=8`

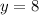
Putting the value of y in equation (2) we get:

`4x+6(8)=96`

`4x+48=96`

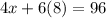
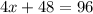
On solving the equation we get:

`x=12`.

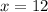Therefore, the price of a senior ticket is $12.