Answer:
x = 3.576 and x = - 3.076
Explanation:
Two functions are given to be, g(x) = 2x² + 3x + 10 and k(x) = 2x + 16.
Now, we have to solve the equation g(x) = 2k(x)
⇒ 2x² + 3x + 10 = 4x + 32
⇒2x² - x - 22 = 0
The expression in the left hand side can not be factorized and therefore we have to use Sridhar Acharya formula which gives the solutions of the equation in the form ax² + bx + c = 0 are given by
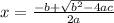 and
and

Therefore, the solutions of the given equation are
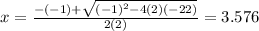
and
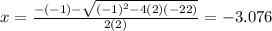 (Answer)
(Answer)