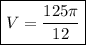Answer:
volume V of the solid
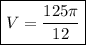
Explanation:
The situation is depicted in the picture attached
(see picture)
First, we divide the segment [0, 5] on the X-axis into n equal parts of length 5/n each
[0, 5/n], [5/n, 2(5/n)], [2(5/n), 3(5/n)],..., [(n-1)(5/n), 5]
Now, we slice our solid into n slices.
Each slice is a quarter of cylinder 5/n thick and has a radius of
-k(5/n) + 5 for each k = 1,2,..., n (see picture)
So the volume of each slice is
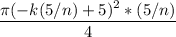
for k=1,2,..., n
We then add up the volumes of all these slices
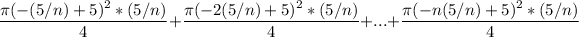
Notice that the last term of the sum vanishes. After making up the expression a little, we get
![\displaystyle(5\pi)/(4n)\left[(-(5/n)+5)^2+(-2(5/n)+5)^2+...+(-(n-1)(5/n)+5)^2\right]=\\\\\displaystyle(5\pi)/(4n)\displaystyle\sum_(k=1)^(n-1)(-k(5/n)+5)^2](https://img.qammunity.org/2020/formulas/mathematics/college/d8n1mbwinzctbp6tgprebdk7esgwxy74tq.png)
But
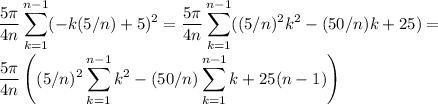
we also know that
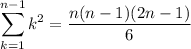
and
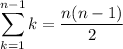
so we have, after replacing and simplifying, the sum of the slices equals
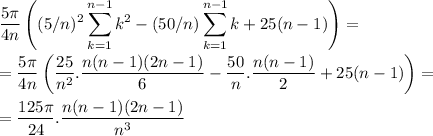
Now we take the limit when n tends to infinite (the slices get thinner and thinner)
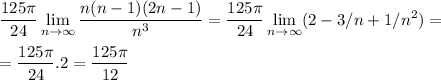
and the volume V of our solid is