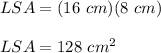2 Answers

Kelvin Schoofs · Answer 1 · 2020-11-26T12:43:13+0000

Answer:
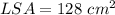
$LSA=128\ cm^2$

Explanation:

The formula for calcualte the Lateral surface area of a prism is:

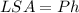
LSA=Ph

Where "P" is the perimeter of the base and "h" is the height of the prism.

Notice that the base is a triangle. Since the perimeter is the sum of its sides, you get that this is:

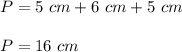
$P=5\ cm+6\ cm+5\ cm\\\\P=16\ cm$

You can identify in the figure that the height is:

$h=8\ cm$

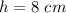
Therefore, you can substitute these values into the formula in order to calculate the Lateral surface area of the given prism. This is:

$LSA=(16\ cm)(8\ cm)\\\\LSA=128\ cm^2$

Please log in or register to add a comment.