Question

In the vicinity of Earth's orbit around the Sun, the energy intensity of sunlight is about 1200 W/m2. What is the approximate magnitude of the electric field in the sunlight? (What you calculate is actually the "root-mean-square" or "rms" magnitude of the electric field, because in sunlight the magnitude of the electric field at a fixed location varies sinusoidally, and the intensity is proportional to E2.)

Answer 1

672.29 W/m²

Step-by-step explanation:

`\epsilon_0` = Permittivity of free space =
`8.85* 10^(-12)\ F/m`

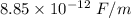
c = Speed of light =
`3* 10^8\ m/s`

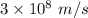
I = Intensity of light = 1200 W/m²

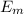`E_m` = Maximum value electric field

Intensity of light is given by

`I=(1)/(2)\epsilon_0cE_m^2\\\Rightarrow E_m=\sqrt{(2I)/(\epsilon_0c)}\\\Rightarrow E_m=\sqrt{(2* 1200)/(8.85* 10^(-12)* 3* 10^8)}\\\Rightarrow E_m=950.765\ N/C`

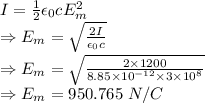
RMS value

`E_r=(E_m)/(\sqrt2)\\\Rightarrow E_r=(950.765)/(\sqrt2)\\\Rightarrow E_r=672.29\ W/m^2`

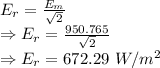
The approximate magnitude of the electric field in the sunlight is 672.29 W/m²