Question

A pilot is traveling at a height of 30,000 feet above ground she looks down at a angle of depression of 6 and spots runway as measured along the ground how many miles away is she from the runway

Answer 1

To find the distance to the runway, we can use trigonometry and create a right triangle using the pilot's height and the angle of depression. Using the tangent function, we can solve for the distance. The pilot is approximately 58.47 miles away from the runway.

Step-by-step explanation:

To find the distance to the runway, we can use trigonometry. The angle of depression of 6 degrees tells us that the runway is below the pilot's line of sight. We can create a right triangle with the pilot's height of 30,000 feet as the opposite side and the distance to the runway as the adjacent side. Using the tangent function, we can solve for the distance:

Tan(6) = Opposite/Adjacent

Tan(6) = 30,000/Adjacent

Adjacent = 30,000/Tan(6)

Using a calculator, we find that the pilot is approximately 308,517 feet away from the runway.

To convert this distance to miles, we divide by 5,280 (since there are 5,280 feet in a mile):

308,517/5,280 ≈ 58.47 miles

Therefore, the pilot is approximately 58.47 miles away from the runway.

Answer 2

Distance between runway and pilot position along the ground is 285430.9336 feet that is 53.9464 miles.

Solution:

Given that

Height of position of pilot from the ground = 30000 feet

Angle of depression when he looks down at runway = 6o

Need to measure along the ground, distance between runway and pilot that is horizontal distance between runway and pilot.

Consider the figure attached below

D represents position of runway.

P represents position of pilot.

PG represents height of position of pilot from the ground that means PG = 30000 feet

PH is virtual horizontal line and HPD is angle of depression means ∠ HPD = 6 degree

AS DG and HP are horizontals, so DG is parallel to HP.

=> ∠ HPD =∠ PDG = 6 degree [ Alternate interior angle made by transversal PD of two parallel lines ]

We need to calculate DG

Consider right angles triangle PGD right angles at G

`\text {As } \tan x=\frac{\text { Perpendicular }}{\text { Base }}`

`\tan \angle \mathrm{PDG}=\frac{\mathrm{PG}}{\mathrm{GD}}`

`\begin{array}{l}{=>\mathrm{GD}=\frac{\mathrm{PG}}{\tan \angle \mathrm{PDG}}} \\\\ {=>\mathrm{GD}=(30000)/(\tan 6^(\circ))=285430.9336}\end{array}`

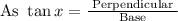
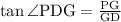
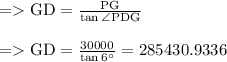
As one foot = 0.000189 miles

`=>285430.9336 \text { feet }=285430.9336 * 0.000189 \text { miles }=53.9464 \text { miles. }`

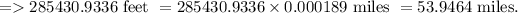
Hence distance between runway and pilot position along the ground is 285430.9336 feet that is 53.9464 miles.