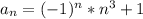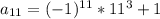Question

1.a.) Find the next four terms: a8,a9,a10,a11


`a_(n)`=0, 9, -26, 65, -124, 217, -342

1.b) Find a direct formula for
`a_(n)`, [Hint: You may want to look at perfect squares, perfect cubes, powers of 2, powers of 3...]

Answer 1

Answers:

1a) The next four terms are: 513, -728, 1001, -1330

1b) The direct formula is
`a_n = (-1)^n*n^3+1`

================================================

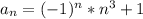
Step-by-step explanation:

It helps to start with part B first. The direct formula will help us find the next four terms in a very efficient manner.

Start with the sequence {0, 9, -26, 65, -124, 217, -342}

Subtract 1 from each term to get this new sequence {-1, 8, -27, 64, -125, 216, -343}, which closely resembles the sequence {1, 8, 27, 64, 125, 216, 343}. This is the sequence of perfect cubes. The only difference is that each term alternates from positive to negative and vice versa.

So we will have an n^3 as part of the equation and also a (-1)^n as part of the equation. The (-1)^n portion allows us to alternate in signs. Put together we have (-1)^n*n^3 so far

The last thing we do is add 1 to this so that we undo the operation "subtract 1" we did earlier to the original list.

Therefore the formula is
`a_n = (-1)^n*n^3+1`

--------------------

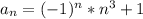
To help verify we have the right formula, plug in n = 1 and we get

`a_n = (-1)^n*n^3+1`

`a_1 = (-1)^1*1^3+1`

`a_1 = 0`

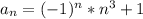
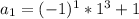
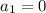
and plug in n = 2 to get

`a_n = (-1)^n*n^3+1`

`a_2 = (-1)^2*2^3+1`

`a_2 = 9`

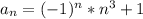
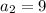
and so on. I'll let you check the other terms

--------------------

Let's find the terms a8,a9,a10,a11

This is simply a matter of plugging n = 8, n = 9, n = 10, and n = 11

Plug in n = 8

`a_n = (-1)^n*n^3+1`

`a_8 = (-1)^8*8^3+1`

`a_8 = 513`

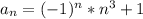
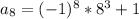
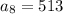
Repeat for n = 9

`a_n = (-1)^n*n^3+1`

`a_(9) = (-1)^9*9^3+1`

`a_(9) = -728`

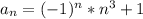
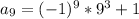
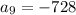
Repeat for n = 10

`a_n = (-1)^n*n^3+1`

`a_(10) = (-1)^(10)*10^3+1`

`a_(10) = 1001`

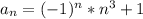
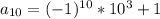
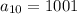
Repeat for n = 11

`a_n = (-1)^n*n^3+1`

`a_(11) = (-1)^(11)*11^3+1`

`a_(11) = -1330`