Question

An explosion causes debris to rise vertically with an initial speed of 120 feet per second. The formula h equals negative 16 t squared plus 120 t describes the height of the debris above the​ ground, h, in​ feet, t seconds after the explosion. When will the debris be 56 feet above the​ ground?

Answer 1

The debris will be at a height of 56 ft when time is 0.5 s and 7 s.

Explanation:

Given:

Initial speed of debris is,
`s=120\ ft/s`

The height 'h' of the debris above the ground is given as:

`h(t)=-16t^2+120t`

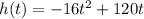
As per question,
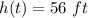`h(t)=56\ ft`. Therefore,

`56=-16t^2+120t`

Rewriting the above equation into a standard quadratic equation and solving for 't', we get:

`-16t^2+120t-56=0\\\textrm{Dividing by -8 throughout, we get}\\(-16)/(-8)t^2+(120)/(-8)t-(56)/(-8)=0\\2t^2-15t+7=0`

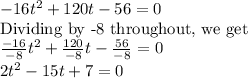
Using quadratic formula to solve for 't', we get:

`t=(-b\pm √(b^2-4ac))/(2a)\\\\t=(-(-15)\pm √((-15)^2-4(2)(7)))/(2(2))\\\\t=(15\pm √(225-56))/(4)\\\\t=(15\pm√(169))/(4)\\\\t=(15\pm 13)/(4)\\\\t=(15-13)/(4)\ or\ t=(15+13)/(4)\\\\t=(2)/(4)\ or\ t=(28)/(4)\\\\t=0.5\ s\ or\ t=7\ s`

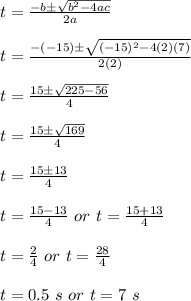
Therefore, the debris will reach a height of 56 ft twice.

When time
`t=0.5\ s` during the upward journey, the debris is at height of 56 ft.

Again after reaching maximum height, the debris falls back and at
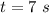`t=7\ s`, the height is 56 ft.