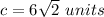Question

Determine the missing measures.
38, a=

Answer 1

a = 6 units

`c= 6√(2)\ units`

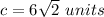
Explanation:

Given:

Let Labelled the diagram first

Δ ABC right angle at ∠ C = 90°

∠ B = 45 °

AB = c

BC = a

AC = 6

To Find:

a =?

c =?

Solution:

In Δ ABC

∠ A + ∠ B + ∠ C = 180°.....{Angle Sum Property of a Triangle}

∴ ∠ A + 45 + 90 = 180°

∴ ∠ A = 180 - 135

∴ ∠ A = 45°

Now ∠ A = ∠ B = 45° in Δ ABC

∴ Δ ABC is an Isosceles Triangle.

∴ Two sides are equal of an Isosceles Triangle.

∴ AC = BC = a = 6 units

Now for c we use Pythagoras theorem

`(\textrm{Hypotenuse})^(2) = (\textrm{Shorter leg})^(2)+(\textrm{Longer leg})^(2)`

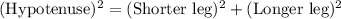
Substituting the given values we get

c² = a² + 6²

c² = 6² + 6²

c² = 36 + 36

c² = 72

∴ c = ±√72

as c cannot be negative

∴
`c = 6√(2)\ units\\`

a = 6 units

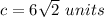
`c= 6√(2)\ units`