Question

Graph f(x), -f(x) and y= 4x ^ 2 cos(x)

Answer 1

See attached image for the graph of the function

Explanation:

Notice that this is the product of a power function (
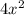`4x^2`) times the trigonometric and periodic function cos(x). So the zeros (crossings of the x axis will be driven by the values at which they independently give zero. That is the roots of the power function (only x=0) and the many roots of the cos function:
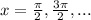`x= (\pi)/(2) , (3\pi)/(2) ,...`, and their nagetiva values.

Notice that the blue curve in the graph represents the original function f(x), with its appropriate zeros (crossings of the x-axis), while the orange trace is that of "-f(x)". Of course for both the zeroes will be the same, while the rest of the curves will be the reflection over the x-axis since one is the negative of the other.