Question

a person throws a rock at 3 M/s down over the edge of a very tall cliff on Earth how far will the rock have fallen in 4 seconds if the rock never hit the bottom?​

Answer 1

The rock will be at 90.4 m from the top of the cliff.

Step-by-step explanation:

The rock is thrown with the “initial velocity” 3 m/s. We need to find how much distance does the rock traveled in 4 seconds (t).

From the “kinematic equations” take

`s=u t+(1)/(2) a t^(2)`

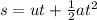
Where, “s” is distance traveled, “u” initial velocity of the object, “t” time the object traveled and “a” acceleration due to gravity is
`9.8 \mathrm{m} / \mathrm{s}^(2).`

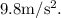
Substitute the given values in the above formula,

`s=3 * 4+(1)/(2) * 9.8 * 4^(2)`

`s=12+(1)/(2) * 9.8 * 16`

`s=12+(1)/(2) * 156.8`

`s=12+78.4`

`s=90.4`

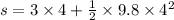
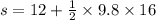
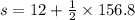
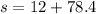
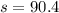
The rock is at height of 90.4 m from the top of the cliff.