Question

Find the number of roots for each equation.
5. 5x4 + 12x3 – x2 + 3x + 5 = 0

Answer 1

The number of roots for equation
`5x^4 + 12x^3 – x^2 + 3x + 5 = 0` is 4 .

Explanation:

Here, the given function polynomial is :

`P(x) : 5x^4 + 12x^3 – x^2 + 3x + 5 = 0`

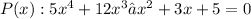
The Fundamental Theorem of Algebra says that a polynomial of degree n will have exactly n roots (counting multiplicity).

Now here, the degree if the polynomial is 4 (highest power of variable x).

So, according to the Fundamental Theorem, the given polynomial can have AT MOST 4 roots, counting Multiplicity.

Hence, the number of roots for equation
`5x^4 + 12x^3 – x^2 + 3x + 5 = 0` is 4 .