Question

Find the exact value of csc (–1020)°.

Answer 1

The correct answer is 6 degrees

Answer 2

By using reference angle, the exact value of csc (-1020)° is
`\frac {-2\sqrt3}{3}`.

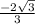How to find the exact value

To find the exact value of csc (-1020)° using the reference angle, first determine the reference angle for -1020°.

To find the reference angle, add or subtract multiples of 360° to bring the angle into the range of 0° to 360°.

-1020° + 360° = -660°

Since -660° is still negative, add another 360°:

-660° + 360° = -300°

Now we have a reference angle of 300°.

The cosecant function (csc) is the reciprocal of the sine function. We know that the sine function is positive in the first and second quadrants, so the cosecant function will be positive in those quadrants.

The exact value of csc(300°) can be found by taking the reciprocal of the sine of 300°:

csc(300°) = 1/sin(300°)

To find the sine of 300°, use the periodicity of the sine function:

sin(300°) = sin(300° - 360°) = sin(-60°)

The sine of -60° is the same as the sine of 60°, but with a negative sign:

sin(-60°) = -sin(60°) =
`\frac {-\sqrt3}{2}`

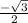
Now, find the reciprocal:

csc(300°) = 1/(-√3/2) =
`\frac {-2}{\sqrt3}`

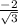
To rationalize the denominator, multiply the numerator and denominator by √3:

csc(300°) =
`\frac {-2}{\sqrt3}` *
`\frac {\sqrt3}{\sqrt3}` =
`\frac {-2\sqrt3}{3}`

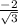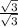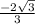
Therefore, the exact value of csc (-1020)° is
`\frac {-2\sqrt3}{3}`.

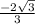Complete question

Use reference angle to find the exact value of csc (–1020)°.