Answer:
The distance between the points ( 5 , - 9 ) and ( - 3 , - 1 ) is 4
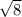
Explanation:
Given points as :
Point A = ( 5 , - 9 )
I.e (x_1 , y_1) = ( 5 , - 9 )
Point B = ( - 3 , - 1 )
I.e( x_2 , y_2) = ( - 3 , - 1 )
Let The distance between points A and B = AB
So From distance formula
Distance AB =
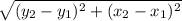
So, Distance AB =
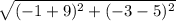
Or, Distance AB =
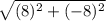
Or, Distance AB =
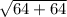
Or, Distance AB =
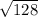
∴ Distance AB = 4
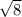
Hence The distance between the points ( 5 , - 9 ) and ( - 3 , - 1 ) is 4
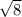 Answer
Answer