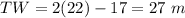Question

In TVW if VW is three meters longer than TV, TW is 20 meters shorter than the sum of VW and TV, and the perimeter of TVW is 74 meters, find the length of VW.

PLEASE EXPLAIN STEPS!!!

Answer 1

The length of VW is
`25\ m`

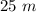
Explanation:

we know that

The perimeter of triangle TVW is equal to

`P=VW+TV+TW`

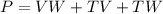
we have

`P=74\ m`

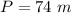
so

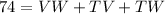`74=VW+TV+TW` -----> equation A

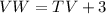`VW=TV+3` ----> equation B

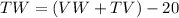`TW=(VW+TV)-20` ----> equation C

substitute equation B in equation C

`TW=(TV+3+TV)-20`

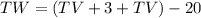
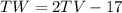`TW=2TV-17` ----> equation D

substitute equation B and equation D in equation A

`74=(TV+3)+TV+(2TV-17)`

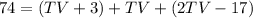
solve for TV

`74=4TV-14`

`4TV=74+14`

`4TV=88`

`TV=22\ m`

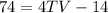
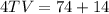
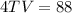
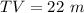
Find the value of VW

`VW=TV+3` ----->
`VW=22+3=25\ m`

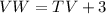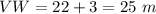
Find the value of TW

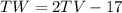`TW=2TV-17` ----->
`TW=2(22)-17=27\ m`