Answer:
The Area of rectangle A is 576 feet² .
Explanation:
Given as :
The width of rectangle A = 16 feet
The Length of rectangle A = 8 feet + The length of rectangle B
The width of rectangle B = 14 feet
Let The length of rectangle B = L feet
So, The Length of rectangle A = 8 feet + L feet
The perimeter of rectangle A + The perimeter of rectangle B = 156 feet
So, 2 × ( Length A + width A ) + 2 × ( Length B + width B ) = 156 feet
Or, 2 × ( 8 + L + 16 ) + 2 × ( L + 14 ) = 156 feet
Or, 2 ×( 24 + L ) + 2 × ( L + 14 ) = 156 feet
Or, 48 + 2 L + 2 L + 28 = 156
Or, 76 L + 4 L = 156
So, 4 L = 156 - 76
Or, 4 L = 80
∴ L =
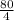 = 20 feet
= 20 feet
So , The Length of rectangle A = 8 feet + 28 feet = 36 feet
And The width of rectangle A = 16 feet
So, Area of rectangle A = Length of rectangle A × width of rectangle A
I.e Area of rectangle A = 36 × 16 = 576 feet²
Hence The Area of rectangle A is 576 feet² . Answer