Question

If cos theta = 3/5 and theta is in the first quadrant, what is sin 2 theta

Answer 1

If cos theta = 3/5 and theta is in the first quadrant, then
`\sin 2 \theta=(24)/(25)`

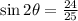
Solution:

Given: cosθ = 3/5 and θ is in first quadrant

We need to find sin2θ

`\text {We know, } \sin ^(2) \theta=1-\cos ^(2) \theta`

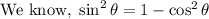
Substitute cosθ in above formula

`\sin ^(2) \theta=1-\left((3)/(5)\right)^(2)`

`\sin ^(2) \theta=1-\left((9)/(25)\right)`

`\begin{array}{l}{\sin ^(2) \theta=(25-9)/(25)} \\\\ {\sin ^(2) \theta=(16)/(25)}\end{array}`

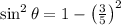
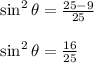
Taking square root on both sides,

`\sin \theta=\pm (4)/(5)`

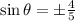
Since, θ is in first quadrant therefore we will choose positive value

`\sin \theta=(4)/(5)`

Let us calculate sin2θ

The formula for sin2θ is given as:

`\sin 2 \theta=2 \sin \theta \cos \theta`

`\sin 2 \theta=2 * (3)/(5) * (4)/(5)=(24)/(25)`

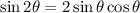
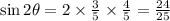
Thus the value of sin 2 theta is found