Answer:
3.0 grams of the element are left after 18 minutes
Explanation:
Recall that an exponential decay that can be studied with the following formula for the amount of material (A) as a function of time (t):
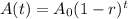
where:
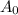 is the starting amount of the substance (in our case 820 grams)
is the starting amount of the substance (in our case 820 grams)
r is the rate of decay (which in our case given as 26.8% can be written in decimal form as 0.268
and t is the time in minutes (in our case t = 18 minutes)
Then we have:
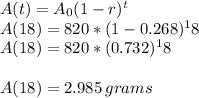
which can be rounded to 3.0 grams